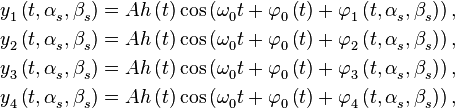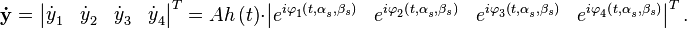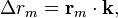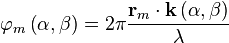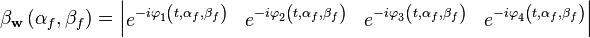Задание 3 к практическим занятиям (ММ РУиС)
Тема занятия: Описание сигналов антенной решетки.
Цели занятия:
- привести пример использования метода комплексных амплитуд;
- изложить методику расчет диаграммы направленности антенной решетки, востребованную при подготовке ко второй лабораторной работе;
- освоить создание и использование собственных функций в MATLAB;
- освоить матричные операции;
- научиться визуализировать поверхности.
Задача 3.1 Сигналы и диаграмма направленности антенной решетки
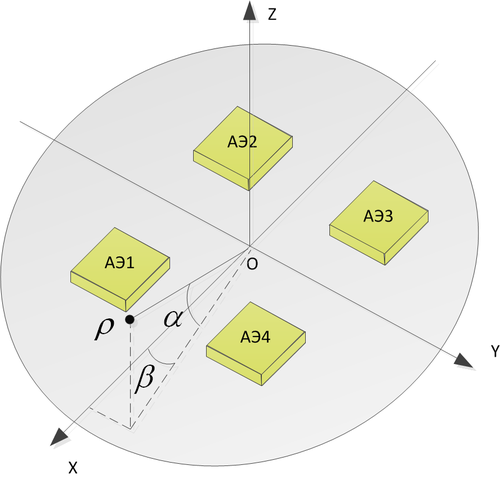
Постановка задачи: Сигнал, приходящий из дальней зоны, принимается системой пространственно разнесенных антенн - антенной решеткой. Размеры антенной решетки значительно меньше постоянной времени корреляции принимаемых сигналов (огибающая, в первом приближении, совпадает для сигналов разных антенн).
Конфигурация антенной решетки - четырехэлементная, с расположением антенных элементов в углах квадрата со стороной, равной половине длине волны.
Построить серию диаграмм направленности при фокусировке в различных направлениях (зенит, отклонение в сторону на 10, 30, 45, 60 градусов).
Комментарии:
Сигналы антенных элементов
Каждая m-я антенна формирует на выходе свой собственный сигнал 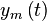 . При фокусировке производят весовое сложение сигналов различных антенн, получая из нескольких сигналов один.
. При фокусировке производят весовое сложение сигналов различных антенн, получая из нескольких сигналов один.
По условию задачи можно пренебречь разностью огибающей для различных точек апертуры антенны. Для ряда практических задач это допущение прекрасно выполняется. Тогда сигналы антенн отличаются только фазой несущей, их математическая модель может быть представлена в виде:
где 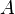 - амплитуда сигналов,
- амплитуда сигналов, 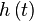 - огибающая,
- огибающая, 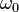 - несущая частота,
- несущая частота, 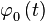 - фаза в начале антенной системы координат OXYZ,
- фаза в начале антенной системы координат OXYZ, 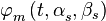 - фазовый набег относительно фазы в начале антенной системы координат для m-й антенны,
- фазовый набег относительно фазы в начале антенной системы координат для m-й антенны, 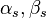 - угол места и азимут направления на источник сигнала.
- угол места и азимут направления на источник сигнала.
В рамках этой задачи удобно применить метод комплексных амплитуд. Тогда модели сигналов преобразуются к виду
![y_{m}^{{}}\left( t \right)= Ah\left( t \right)\operatorname{Re}\left[ e_{{}}^{i\left( \omega _{0}^{{}}t+\varphi _{0}^{{}}\left( t \right) \right)}e_{{}}^{i\varphi _{m}^{{}}\left( t, \alpha _{s}^{{}},\beta _{s} \right)} \right]](/images/math/b/1/2/b1235c5aa0b5d51f3632f800e880fe08.png) ,
,
обозначим
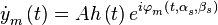 - комплексная амплитуда сигнала m-ой антенны.
- комплексная амплитуда сигнала m-ой антенны.
Составим вектор из комплексных амплитуд сигналов различных антенн
Вектор комплексных амплитуд при приеме образуется после гетеродинирования сигналов (в передающих устройствах последовательность обратная).
Связь фазовых набегов с направлением на источник сигнала
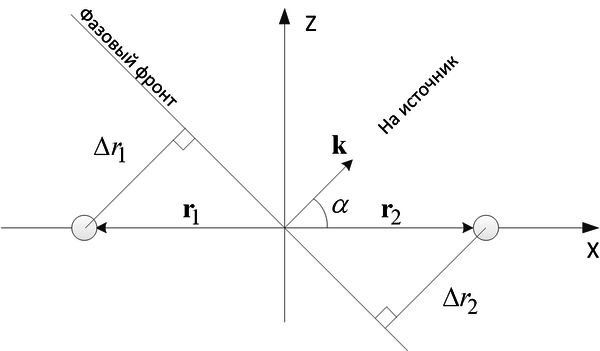
Фазовый набег относительно фазы в начале антенной системы координат определяется положением антенного элемента и направлением прихода сигнала. Его легко рассчитать зная орт 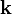 на источник и радиус-вектор
на источник и радиус-вектор 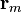 антенного элемента.
антенного элемента.
Разность хода фазового фронта сигнала 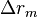 есть скалярное произведение орта и радиус-вектора точки пространства
есть скалярное произведение орта и радиус-вектора точки пространства
фазовый набег связан с разностью хода фазового фронта через длину волны несущей сигнала
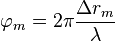 .
.
Для m-oй антенны и направления 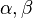 получаем выражение
получаем выражение
Алгоритм фокусировки
При фокусировке антенны в направлении углов 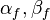 производится умножение вектора-строки фокусировки на вектор-столбец комплексных сигналов
производится умножение вектора-строки фокусировки на вектор-столбец комплексных сигналов
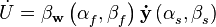 .
.
Вектор фокусировки определяется ожидаемыми фазовыми набегами для направления фокусировки
Диаграмма направленности
Характеристикой направленности называют зависимость нормированной комплексной амплитуды
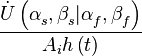 на выходе системы пространственной обработки от направления прихода пробного сигнала
на выходе системы пространственной обработки от направления прихода пробного сигнала 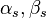 при заданном направлении фокусировки
при заданном направлении фокусировки 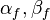 . Здесь
. Здесь 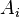 - амплитуда одного сигнала на выходе всенаправленной антенны.
- амплитуда одного сигнала на выходе всенаправленной антенны.
Функция
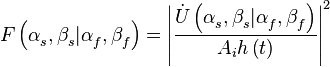 называется диаграммой направленности.
называется диаграммой направленности.
Для принятой модели сигналов диаграмма направленности определяется выражением:
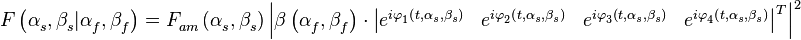 ,
,
где 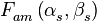 - диаграмма направленности одного антенного элемента.
- диаграмма направленности одного антенного элемента.
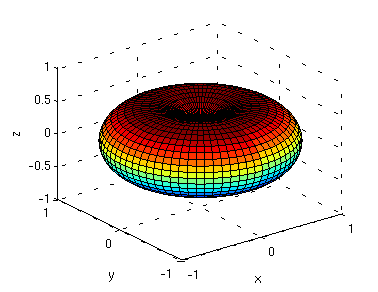
Вывод диаграммы направленности в трехмерном виде
Результатом вычислений диаграммы направленности является массив значений 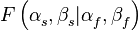 для угла
для угла 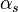 от -180 до 180 градусов,
от -180 до 180 градусов, 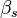 от -90 до 90 (данный выбор диапазона углов не соответствует традиционному определению сферических координат, зато удобен для вывода диаграммы направленности):
от -90 до 90 (данный выбор диапазона углов не соответствует традиционному определению сферических координат, зато удобен для вывода диаграммы направленности):
beta = deg2rad(-90:2:90);
...
F
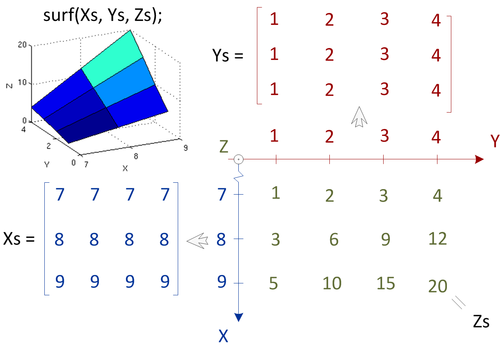
Для задания поверхности недостаточно задать массивы координат её точек, т.к. нужна информация о том, какие точки являются соседними - что с чем соединять. Поэтому в MATLAB используются не три вектора координат, а три матрицы, задающие сетку параметров.
Для "растягивания" векторов координат абсцисс и ординат используется функция meshgrid
Значения 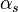 ,
, 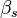 ,
, 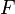 задают три координаты в сферической системе координат. В MATLAB доступны функции построения поверхностей в прямоугольной декартовой системе координат, поэтому перед построением необходимо произвести соответствующее преобразование. Для преобразования из сферической в прямоугольную систему существует функция
задают три координаты в сферической системе координат. В MATLAB доступны функции построения поверхностей в прямоугольной декартовой системе координат, поэтому перед построением необходимо произвести соответствующее преобразование. Для преобразования из сферической в прямоугольную систему существует функция [x, y, z] = sph2cart(beta_m, alpha_m, F), производящая отображение:
y = F .* cos(alpha_m) .* sin(beta_m);
z = F .* sin(alpha_m);
Для вывода поверхности используется функция surf(x, y, z)
surf(x, y, z);
xlabel('x'); ylabel('y'); zlabel('z');
Для лучшего восприятия следует сделать равные пределы по всем трем осям
maxc = max( [max(max(x)) max(max(y)) max(max(z))] );
xlim([minc maxc]); ylim([minc maxc]); zlim([minc maxc]);
Например, для четвертьволнового вибратора
вывод диаграммы направленности