Задание 4 к практическим занятиям (ММ РУиС)
Материал из SRNS
Версия от 23:00, 1 апреля 2014; Korogodin (обсуждение | вклад)
Тема занятия: Преобразование Фурье. Режектор узкополосных помех.
Цели занятия:
- научиться выполнять преобразование Фурье в MATLAB;
- научиться правильно интерпретировать результаты дискретного преобразования Фурье;
- рассмотреть пример использования ДПФ в алгоритмах обработки сигналов;
- научиться применять весовые окна.
Задача 4.1
Постановка задачи:
Производится обработка отсчетов АЦП в радиоприемнике. Модель полезного сигнала:
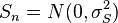 ,
,
частота дискретизации 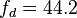 МГц.
МГц.
Помимо полезного сигнала присутствует аддитивная гармоническая помеха с частотой 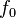 и мощностью на
и мощностью на 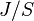 = 30 дБ выше полезного сигнала.
= 30 дБ выше полезного сигнала.
Сигнал АЦП обрабатывается режектором узкополосных помех на базе быстрого преобразования Фурье (объем выборки  = 64).
= 64).
Требуется построить осциллограммы и спектры сигналов на входе и выходе режектора для различных значений 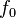 , с использования оконной обработки (окно Парзена) и без неё.
, с использования оконной обработки (окно Парзена) и без неё.
Пример листинга программы:
clear all; clc; close all;
use_window = 0;
Fd = 44.1e6; % Hz
N = 64;
T = 1/Fd * N;
t = ( (1:N) - 1 ) / Fd;
f = ( (1:N) - 1 ) / T;
stdS = 8; % RMS of signal
JtoS_dB = 30; %dB, jammer-to-signal
JtoS_amp = 10^(JtoS_dB/20);
S = randn(1, N) * stdS; % Signal
f0 = Fd / 8; % Jammer intermediate frequency
A_jam = stdS * JtoS_amp; % Amplitude of jam
Jam = A_jam * sin(2*pi*f0*t); % Jam
y = S + Jam; % ADC output
% Graphics
figure(1);
subplot(5,2,1)
stem(t*1e6, S)
xlabel('t, \mus');
ylabel('S');
subplot(5,2,2)
stem(f/1e6, abs(fft(S)))
xlabel('f, MHz');
ylabel('fft(S)');
subplot(5,2,3)
stem(t*1e6, Jam)
xlabel('t, \mus');
ylabel('Jam');
subplot(5,2,4)
stem(f/1e6, abs(fft(Jam)))
xlabel('f, MHz');
ylabel('fft(Jam)');
subplot(5,2,5)
stem(t*1e6, y)
xlabel('t, \mus');
ylabel('y');
yf = fft(y);
subplot(5,2,6)
stem(f/1e6, abs(yf))
xlabel('f, MHz');
ylabel('fft(y)');
h = 400;
signal_clear = 0;
if use_window
yw = y .* parzenwin(N)';
else
yw = y;
end
yfw = fft(yw);
subplot(5,2,7)
stem(t*1e6, yw);
xlabel('t, \mus');
ylabel('y after window');
subplot(5,2,8)
stem(f/1e6, abs(yfw));
xlabel('f, MHz');
ylabel('fft(y after window)');
yf_rej = yfw;
for k = 1:N
if abs(yf_rej(k)) > h
yf_rej(k) = 0;
else
yf_rej(k) = yf_rej(k);
end
end
y_rej = ifft(yf_rej);
subplot(5,2,9)
stem(t*1e6, real(y_rej));
xlabel('t, \mus');
ylabel('y after rejector');
subplot(5,2,10)
stem(f/1e6, abs(fft(y_rej)));
xlabel('f, MHz');
ylabel('fft(y after rejector)');
use_window = 0;
Fd = 44.1e6; % Hz
N = 64;
T = 1/Fd * N;
t = ( (1:N) - 1 ) / Fd;
f = ( (1:N) - 1 ) / T;
stdS = 8; % RMS of signal
JtoS_dB = 30; %dB, jammer-to-signal
JtoS_amp = 10^(JtoS_dB/20);
S = randn(1, N) * stdS; % Signal
f0 = Fd / 8; % Jammer intermediate frequency
A_jam = stdS * JtoS_amp; % Amplitude of jam
Jam = A_jam * sin(2*pi*f0*t); % Jam
y = S + Jam; % ADC output
% Graphics
figure(1);
subplot(5,2,1)
stem(t*1e6, S)
xlabel('t, \mus');
ylabel('S');
subplot(5,2,2)
stem(f/1e6, abs(fft(S)))
xlabel('f, MHz');
ylabel('fft(S)');
subplot(5,2,3)
stem(t*1e6, Jam)
xlabel('t, \mus');
ylabel('Jam');
subplot(5,2,4)
stem(f/1e6, abs(fft(Jam)))
xlabel('f, MHz');
ylabel('fft(Jam)');
subplot(5,2,5)
stem(t*1e6, y)
xlabel('t, \mus');
ylabel('y');
yf = fft(y);
subplot(5,2,6)
stem(f/1e6, abs(yf))
xlabel('f, MHz');
ylabel('fft(y)');
h = 400;
signal_clear = 0;
if use_window
yw = y .* parzenwin(N)';
else
yw = y;
end
yfw = fft(yw);
subplot(5,2,7)
stem(t*1e6, yw);
xlabel('t, \mus');
ylabel('y after window');
subplot(5,2,8)
stem(f/1e6, abs(yfw));
xlabel('f, MHz');
ylabel('fft(y after window)');
yf_rej = yfw;
for k = 1:N
if abs(yf_rej(k)) > h
yf_rej(k) = 0;
else
yf_rej(k) = yf_rej(k);
end
end
y_rej = ifft(yf_rej);
subplot(5,2,9)
stem(t*1e6, real(y_rej));
xlabel('t, \mus');
ylabel('y after rejector');
subplot(5,2,10)
stem(f/1e6, abs(fft(y_rej)));
xlabel('f, MHz');
ylabel('fft(y after rejector)');